| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- BFS
- JS
- 그리디
- 함수
- Linux
- 웹개발
- 문자열
- npm
- 최단거리
- node.js
- 알고리즘
- 프리코스
- 우테코
- dfs
- 코딩테스트
- Sort
- express
- 백준
- 프로그래머스
- 자바스크립트
- JavaScript
- 우아한테크코스
- 그래프
- 코테
- 파이썬
- 프론트엔드
- 고득점kit
- Python
- OpenCV
- JetsonNano
- Today
- Total
공대생
백준 1074 Z Python 본문
문제설명
한수는 크기가 2^N × 2^N인 2차원 배열을 Z모양으로 탐색하려고 한다. 예를 들어, 2×2배열을 왼쪽 위칸, 오른쪽 위칸, 왼쪽 아래칸, 오른쪽 아래칸 순서대로 방문하면 Z모양이다.

N > 1인 경우, 배열을 크기가 2^(N-1) × 2^(N-1)로 4등분 한 후에 재귀적으로 순서대로 방문한다.
다음 예는 2^2 × 2^2 크기의 배열을 방문한 순서이다.

N이 주어졌을 때, r행 c열을 몇 번째로 방문하는지 출력하는 프로그램을 작성하시오.
다음은 N=3일 때의 예이다.

제한사항

- 1 ≤ N ≤ 15
- 0 ≤ r, c < 2N
입력
첫째 줄에 정수 N, r, c가 주어진다.
출력
r행 c열을 몇 번째로 방문했는지 출력한다.
예제
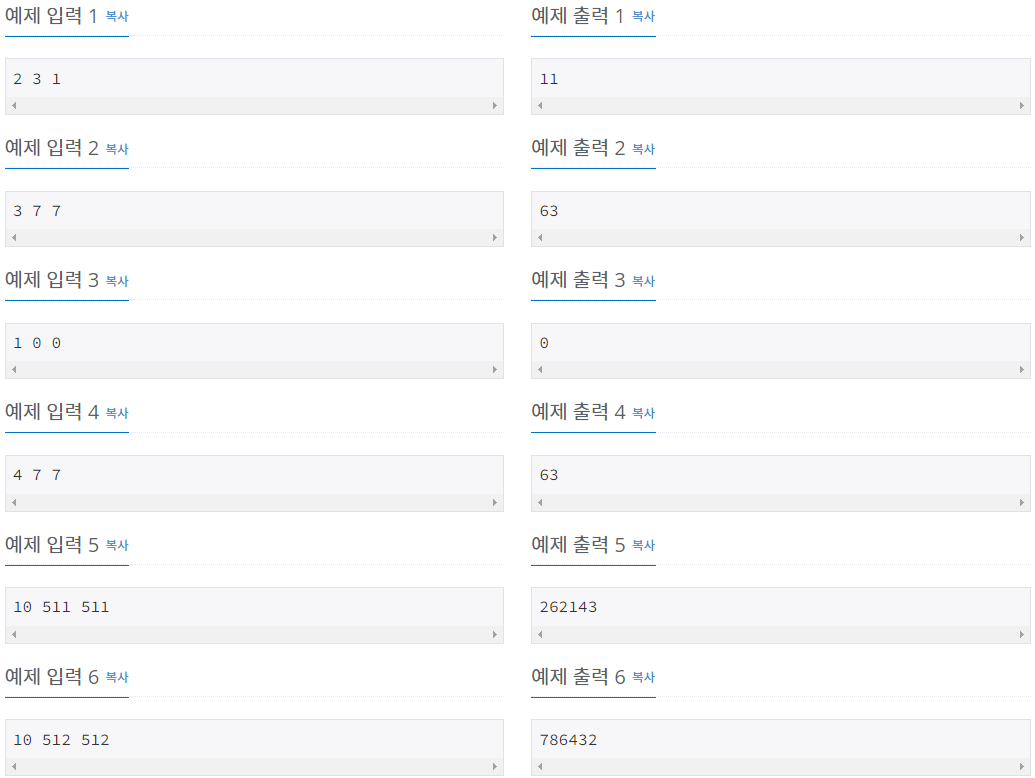
이 문제의 key포인트
-> N > 1인 경우, 배열을 크기가 2^(N-1) × 2^(N-1)로 4등분 한 후에 재귀적으로 순서대로 방문한다.
문제를 오해하기 쉽다.
N이 주어지고 N이 1보다 크면 2^(N-1) × 2^(N-1)로 4등분 한 후, r과 c가 해당하는 사분면에서
다시 2^(N-2) × 2^(N-2)로 4등분한 후, r과 c가 해당하는 사분면에서
다시 2^(N-3) × 2^(N-3)로 4등분한 후,
.
.
.
이렇게 재귀적으로 r과 c가 포함된 사분면을 분할해서 순서를 찾아내는 문제다.
자료구조 및 알고리즘: 분할정복, 재귀
문제풀이
첫번째 풀이
코드(틀린코드, 틀렸습니다)
N, r, c = map(int, input().split())
length = 2 ** N - 1
half = 2 ** (N-1) - 1
count = 0
def counting(start_r, start_c):
cnt = 0
# 몇번째 Z인지 찾기
dif_r = r - start_r
dif_c = c - start_c
# 현재 위치 전 Z까지의 개수
num = (dif_r // 2) * ((half + 1) // 2) + (dif_c // 2)
cnt += num * 4
# 현재 4개짜리에서 몇번째인지 찾기
# 현재 위치 시작위치 찾기 -> num+1번째 Z의 시작위치
s_r = start_r + (dif_r // 2) * 2
s_c = start_c + (dif_c // 2) * 2
diff_r = r - s_r
diff_c = c - s_c
if diff_r == 0 and diff_c == 0:
cnt += 1
elif diff_r == 0 and diff_c == 1:
cnt += 2
elif diff_r == 1 and diff_c == 0:
cnt += 3
else:
cnt += 4
return cnt
half_num = (half+1) * (half+1)
# 1사분면
if 0 <= r <= half and 0 <= c <= half:
# 개수세기
count += counting(0, 0)
# 2사분면
elif 0 <= r <= half and half < c <= length:
count += half_num
count += counting(0, half + 1)
# 3사분면
elif half < r <= length and 0 <= c <= half:
count += 2 * half_num
count += counting(half + 1, 0)
# 4사분면
else:
count += 3 * half_num
count += counting(half + 1, half + 1)
print(count - 1) # 카운팅을 0부터 시작하므로처음에 이 문제를 잘못 이해하고 있었다. 완전 틀린 개념으로 접근했는데 예제는 어떻게 다 맞았는지 모를 일


처음에만 사분면을 구분하고 그 안에서는 2^(N-1) 길이만큼 Z모양을 돈 후 아래 칸으로 내려오는건줄 알았는데 N이 1이 될 때까지 재귀적으로 사분면을 나누어줘야 하는 문제였다. 따라서 위의 코드에는 반례가 존재한다.
# 반례
입력: 5, 22, 22
-> 정답: 828
-> 현재 답: 876
여기서 분할정복을 이용해야겠다고 생각했다. 같은 유형의 문제로 계속해서 나누는 문제이고 각 문제들은 독립적이기 때문이다.
두번째 풀이
코드(완성코드)
# BOJ 1074 Z
# 72ms
# 30840KB
N, r, c = map(int, input().split())
count = 0
# 분할정복(재귀)
def counting(start_r, start_c, n): # r, c 시작점, N
global count
length = 2 ** n - 1
half = 2 ** (n-1) - 1
if n == 1:
# 거기서부터 좌표 찾으면서 누적
if r == start_r and c == start_c:
count += 1
elif r == start_r and c == start_c + 1:
count += 2
elif r == start_r + 1 and c == start_c:
count += 3
else:
count += 4
return
half_num = (half+1) * (half+1)
# 1사분면
if start_r <= r <= start_r + half and start_c <= c <= start_c + half:
# 다시 쪼개기
counting(start_r, start_c, n - 1)
# 2사분면
elif start_r <= r <= start_r + half and start_c + half < c <= start_c + length:
count += half_num
counting(start_r, start_c + half + 1, n - 1)
# 3사분면
elif start_r + half < r <= start_r + length and start_c <= c <= start_c + half:
count += 2 * half_num
counting(start_r + half + 1, start_c, n - 1)
# 4사분면
else:
count += 3 * half_num
counting(start_r + half + 1, start_c + half + 1, n - 1)
counting(0, 0, N)
print(count - 1) # 카운팅을 0부터 시작하므로n > 1이면 r, c가 존재하는 사분면에서 다시 재귀적으로 사분면을 쪼개도록 했고
n이 1일땐 Z에서 몇번째 위치인지 카운팅하고 return하도록 구현했다.
'스터디 > 백준' 카테고리의 다른 글
| 백준 1260 DFS와 BFS Python (0) | 2022.05.30 |
|---|---|
| 백준 1107 리모컨 Python (0) | 2022.05.25 |
| 백준 1012 유기농배추 Python (0) | 2022.05.21 |
| 백준 18111 마인크래프트 Python (0) | 2022.05.19 |
| 백준 11401 이항 계수 3 Python (0) | 2022.03.06 |




