백준 11401 이항 계수 3 Python
11401 - 이항 계수 3
이항계수를 계산하는 공식은 아래와 같다.

이 문제에서 우리가 구하려는 것은 해당 조합 값을 P(1000000007)로 나눈 나머지이다.
무턱대고 위의 공식을 이용해 이항계수를 구하고 P로 나눈 나머지를 출력하면 당연하게도 시간초과가 뜬다.

큰 수를 계산할 때 시간이 걸린다는 이유로 이런 식으로 식을 풀게되면 분모가 0이 되는 경우가 있어서 런타임에러(/ by zero) 가 뜨게된다. 따라서 해당식을 분수형태가 아닌 정수의 곱으로 표현해야할 필요가 있다.
이때 필요한 게 페르마의 소정리이다.
페르마의 소정리
p가 소수이고 a가 정수일 때, 다음을 만족한다는 것이다.

a^p와 a가 합동이라고 하는데 정수론에서는 p로 나눈 나머지가 동일하다는 뜻으로 쓰인다.
( 예를 들어 5^3과 5를 각각 3으로 나누면 나머지가 2로 동일한 것이다. )
해당 식을 양변을 a로 나눠서 변형시키면
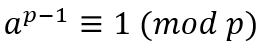
다시 양변을 a로 나누면

이를 통해 a의 역원(a^-1)이 a^(p-2)라는 것을 구할 수 있다. (아래에서 계산할 때 이 값이 필요하다)
우리가 구하려고 하는 것

위의 식에서 N!을 A라 하고 K!(N-K)!을 B라고 하자. 식은 A / B % P가 되고 여기서 분수를 제곱식으로 표현하면 다음 식이 된다.

여기서 우리가 페르마의 소정리에서 구한 역원이 필요하다. 역원(B^(-1) = B^(P-2))을 대입하면

따라서 우리가 구하려는 식을 위의 식에서 아래 식으로 변형할 수 있다. 이렇게 하면 정수를 P로 나눈 나머지를 찾는 것이기 때문에 계산이 훨씬 수월해진다.

최종구현
팩토리얼 함수와 P-2번 거듭제곱을 할 power 함수를 구현하였다.
주의점: 팩토리얼 함수를 재귀를 이용해 구현하면 런타임에러(RecursionError) 가 난다. 따라서 팩토리얼은 그냥 for문을 이용해 구현하고 이때 수를 하나씩 곱할 때마다 P로 나눈 나머지를 temp로 저장해야 시간초과가 나지 않는다.
최종문제풀이 코드
# BOJ 11401
# 1244ms
# 30864KB
import sys
input = sys.stdin.readline
N, K = map(int, input().split())
P = 1000000007
# 재귀로 구현하면 런타임에러 (RecursionError)
# 팩토리얼 곱할 때마다 P로 나눠줘야 시간초과 해결
def factorial(n):
temp = 1
for i in range(2, n+1):
temp *= i
temp %= P
return temp
# 거듭제곱
result = 1
def power(n):
global result
if n == 1:
result = A % P
return result
else:
if n % 2 != 0:
n = n // 2
temp = power(n) % P
result = temp * temp * power(1)
else:
n = n // 2
temp = power(n) % P
result = temp * temp
return result
A = factorial(K) * factorial(N-K) % P
final = (factorial(N) * power(P-2)) % P
print(final)
참고링크